A Reductive Explanation for Recent Changes in Math Pedagogy

Yes, your kid's math homework is weird. Is it worth it? Hard to say

two people who learned math in dramatically different policy and pedagogical contexts, trying to understand one another

Everyone has heard stories about how math instruction has changed since today’s parents were in school - if not for the worse, then at least for the weird. These complaints represent a genuine phenomenon; math instruction really has changed. This perception has grown a great deal in the past decade as Common Core (RIP, more or less) and many state-specific curriculum reforms have pushed emerging pedagogical philosophies from academic journals into the classroom¹. What’s going on?

First, we should distinguish recent changes from “New Math,” a somewhat-common reference point when I was young. Those changes, similar in the sense of being clumsily adopted with good intentions and pressure from above, took place several generations earlier than what I’m referring to now, mostly in the 1960s. It was all a big failure, at least in public opinion.

via

Here’s the nut of what’s been happening in the past decade. This evolution in teaching math in the United States stems from both a pragmatic problem and a theoretical justification. The problem is that math scores in the United States don’t improve in general and particularly don’t in middle and high school, when judged on a variety of metrics. (I refuse to say that American math skills are bad, as when we make responsible comparisons in historical and international terms they simply aren’t, but that’s for another time.) Many people have been vexed in particular by the failure of improvements in 4th grade NAEP scores to be matched when that cohort ages into 8th grade. (The kids by and large won’t be the same kids taking the tests, as it’s a sampled and stratified test, but for that very reason it shouldn’t matter.) There’s a 4th grade advantage in absolute terms; in 2019, 41% of 4th graders and 34% of 8th graders scored proficient in math in 2019. But there’s also been more difficulty showing year over year progress in 8th grade too. Here’s an elegant visual demonstration of the 4th vs 8th grade slowdown:

source; graphed lines show improvement relative to 1996

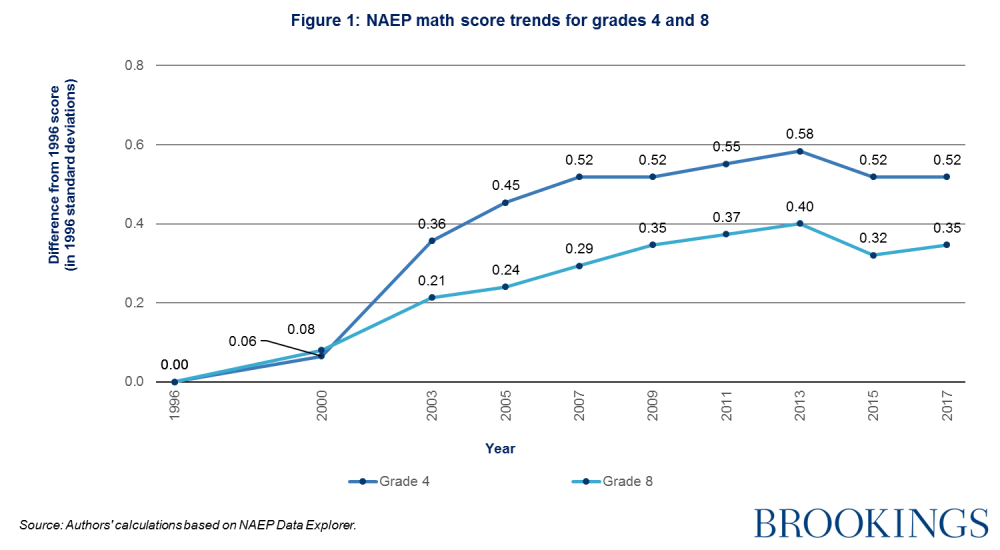
Since it often seems like nothing works to improve large-scale quantitative metrics, the bumps in 4th grade numbers are the kind to inspire many dissertations and policy papers. There’s an urge to say “aha! We finally figured out this learning thing!” But when the kids responsible for the 4th grade scores age into the 8th grade cohort and don’t keep up the pace it produces political and policy pressure to find out why and fix the problem. My own assumption, as regular readers might guess, is that the talent curve simply asserts itself more heavily in advanced math - more people are likely to reach the limits of their natural ability in Algebra II than when learning long division. But our entire educational policy discussion is based on the notion that there is no such thing as natural talent, so that conclusion can’t be reached.

Anyway, academics and policy types felt compelled by this state of affairs to say “how is later math different than earlier?” And what some influential people concluded was that the latter has more “abstract” math than the former; that is, earlier and later math are not just different in difficulty and complexity but different in kind in that math in later grades requires not just arithmetic skills (number crunching, grinding, etc) but quantitative reasoning. Reasoning, that is, about the nature of math above its application in a consistent process of calculation. Some people in ed research call this reasoning “numbers sense.” What certain influential people in ed policy intuited was that the problem with getting test scores to grow in middle and high school stemmed from students lacking prerequisite knowledge in those abstract skills. We’re trying to ramp our kids up too much, too quickly when they make the turn around middle school age², or so the thinking goes. The cry therefore went out to integrate numbers sense into math for younger children. Here’s an example of such an argument from when this position had started to gather a lot of steam. And that’s how you get 5th graders doing what are essentially mathematical proofs, and that’s how you get parents staring in numb incomprehension at their kid’s homework.

(It’s perhaps worth noting that there’s also been something of a similar push for more quantitative reasoning in higher education. This is, as you like it, a demonstration of symmetries in thinking across the entire educational system or a function of the faddishness and gimmickry inherent to pedagogy discourse.)

Now, you can find math experts and education experts who very passionately reject some of the assumptions here. For instance, there are those who question the very basis of all of this and will insist that the arithmetic aspects of math simply are the conceptual aspects and that such an artificial dichotomy doesn’t prepare children for advanced math³, where the division entirely collapses. I am not enough of a math person to weigh in on this particular debate. More tangibly there’s the problem with selling these changes to the most activist stakeholders, the parents. For the teachers and administrators who are the pointy end of the stick for this kind of pedagogical change, and relevant to politics, this development introduces lots of new foreign-seeming vocabulary that parents hate, leading to situations where they bang their heads against a wall wondering why their kid is suddenly obsessed with which “bins” certain numbers go in. And the more abstract focus also introduces a fixation on process over result, again frustrating parents, who somewhat understandably wonder why it matters how their kid solves a division question so long as they get it right.

It would probably be better for marketing purposes if I had some passionate criticism or defense of this broad change, but I don’t. I think anyone telling you that we know one way or another if this is working or will work, in an empirical sense, is way out ahead of their skis. My generic prediction is always that while pedagogical developments can have small-scale changes that are meaningful for individual kids, regardless of pedagogical technique we’ll almost certainly get the same general performance distribution that more-or-less matches the talent distribution. (I don’t believe, to pick an obvious point of emphasis, that racial achievement gaps can be solved in the classroom; they're bigger than that.) But who knows? I do have personal experience as someone who did math effortlessly from K-6 and then saw my math grades fall off a cliff in the years that followed. I certainly had some biographical confounds there, but I think there’s something to the idea that there’s a transition in math around that age that goes deeper than a linear increase in computing complexity and which I didn’t feel prepared for.

On the other hand, all of this should remind us of a basic element of education, which is that most children, or at least children fortunate enough to have involved parents, are inevitably going to be learning a lot at home as well as at school And so there’s a permanent baked-in complication with major pedagogical changes: they will frequently create a scenario where parent and child are using very different vocabularies and techniques to approach the same questions. That’s the kind of pain point that can inspire parents to apply pressure on administrators and politicians. That might not sound like a big deal, but exactly that kind of parent uprising has contributed to (though not unilaterally caused) the reversal of political fortunes for K-12 census testing. This increased difficulty for parents, tutors, workers in afterschool programs, etc. compounds the dissatisfaction of teachers, who have been justifiably complaining for decades that endless policy changes and attendant pedagogical evolutions force them into constant training and compel them to abandon principles that have worked for them for years. Are these reasons to oppose pedagogical evolution in general? No, obviously not. But they are complications to consider.

For the record, as tempting as it to just lay this all on the feet of Common Core (and in a roundabout way NCLB), these widespread curriculum changes have many fathers, and some states would be pushing them regardless of the (declining) influence of Common Core. And it is worth saying that most of the people involved are making these changes out of good-faith belief that they will result in better teaching. (As were most of the people behind the Common Core, as misguided a project as it might have ultimately been.) Unfortunately they can't currently buttress that faith with evidence.

In the short term, I can’t tell you if puzzling over the bins and bunches and grids in your child’s math homework will be worth it. Perhaps time will tell. Good luck.

1. Via heavy-handed teacher in-services which can mean a lot or nothing in practice depending on the specific system, superintendent, or principal.

2. I would argue that this age represents an inflection point in several ways; it’s here, for example, that many practitioners would say that you can first really identify the truly gifted. Which again speaks to the reality of talent but, well, you know.

3. Most children will never grow up to achieve proficiency in genuinely advanced math regardless of how they are taught, but I digress.