norm referencing, criterion referencing, and ed policy
I want to talk a bit about a distinction between different types of educational testing/assessment and how they interface with some basic questions we have about education policy. The two concepts are norm referencing and criterion referencing.
Criterion Referencing
Why do we perform tests? What are their purpose? One common reason is to ensure that people are able to perform some sort of an essential task. Take a driver's test. The point is to make sure that people who are on the roads possess certain minimal abilities to safely pilot a car, based on social standards of competence that are written into policy. While we might understand that some people are better or worse drivers than others, we're not really interested in using a driver's test to say who is adequate, who is good, and who is excellent. Rather we just want to know: do you meet this minimal threshold? The name for that kind of test is a criterion referenced test. We have some criterion (or criteria) and we check and see if the people taking the test fulfill them. Sometimes we want these tests to be fairly generous; society couldn't function, in many locales, if a majority of competent adults couldn't pass a driver's test. On the other hand, we probably want the benchmarks for, say, running a nuclear reactor to be fairly strict. The social costs would here be higher for a test that was too lenient rather than too strict. In either case, though, our interest is not in discriminating between different individuals to a fine level of gradation, particularly for those who are clearly good enough or clearly not. Rather we just want to know: is the test taker competent to perform the real-world task?
Norm Referencing
Criterion referencing depends on, well, the existence of a criterion. That is, there has to be some sort of benchmark or goal that the test taker will either reach or not. What would it mean to have a criterion referenced test for, say, college readiness? We can certainly imagine a set benchmark for being prepared for college, and we'd probably like to think that there's some minimal level of preparation that's required for any college-bound student. But in a broader sense we are probably aware that there is no one set criterion that would work given the large range of schools and students that "college readiness" reflects. What's more, we also know that colleges are profoundly interested in relative readiness; elite colleges spend vast amounts of money attracting the most highly-qualified students to campus.
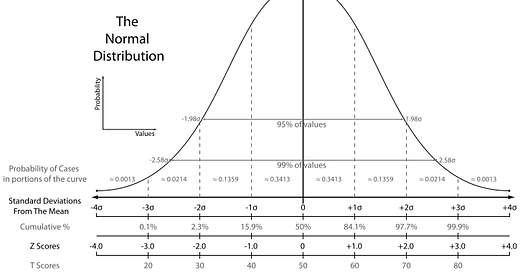
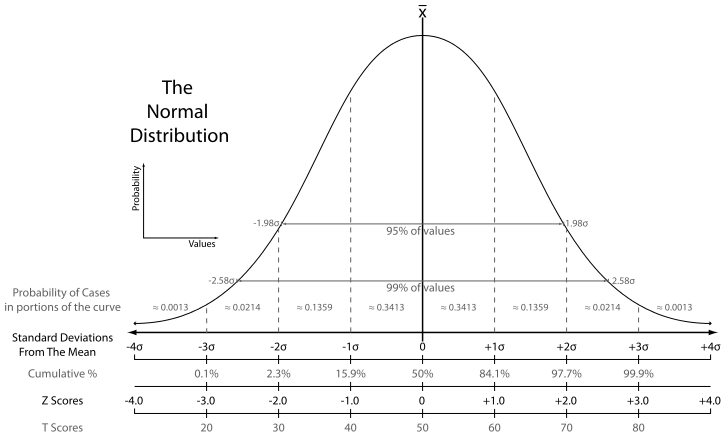
For that we need to use tests like the SAT and ACT which are not oriented around fulfilling a given criterion but for creating a scale of test-takers and being able to discriminate between different students in exacting detail. We need, that is, norm referenced tests. When we say "norm" here we mean in comparison to others, to an average and to quintiles, and in particular to the normal distribution. I don't want to get too into the weeds on that big topic, for those who aren't already versed in it. Suffice to say for now that the normal distribution is a very common distribution of observed values for all sorts of naturally-occurring phenomenon that have a finite range (that is, a beginning and an ending) and which are affected by multiple variables. The ideal normal distribution looks like this:
The big center line in there is the mean, median, and mode - that it, the arithmetic average, the line that divides one half of the data from the other, and the observation that occurs most. As you can see, in a true normal distribution the observations fall in very particular patterns relative to the average. In particular, the further away we go from the average, the less likely we are to find observations, again in predictable quantitative relationships. When we talk about something changing relative to a standard deviation, using that statistic (actually a measure of spread) as a measure of distance or extremity, we're doing so in relation to the normal distribution. Tests like the SAT and ACT, GRE, IQ tests, and all manner of other tests used for the purpose of screening applicants for some finite number of slots use norm referencing.
Why? Again, think about what we're trying to accomplish with norm referencing. I want to give a test to be able to say that test taker X is better than test taker Y but worse than test take Z. But we also want to be able to say where they each fall relative to the mass of data. Norm referencing allows us to make meaningful statements about how someone will perform relative to others, and this in turn gives us information about how to, for example, select people for our scarce admissions slots at an exclusive college.
As Glenn Fulcher puts it in his (excellent) book Practical Language Testing:
As we move away from the mean the scores in the distribution become more extreme, and so less common. It is very rare for test takers to get all items correct, just as it is very rare for them to get all items incorrect. But there are a few in every large group who do exceptionally well, or exceptionally poorly. The curve of normal distribution tells us what the probability is that a test taker could have got the score they have, given the place of the score in a particular distribution. And this is why we can say that a score is ‘exceptional’ or ‘in the top 10 per cent’, or ‘just a little better than average.
(Incidentally, it's a very common feature of various types of educational, intelligence, and language testing that scores become less meaningful as the move towards the extremes. That is, a 10 point difference on a well-validated IQ test means a lot when it comes to the difference between a 95 and a 105, but it means much less when it comes to a difference between 25 and 35 or 165 and 175. Why? In part because outliers are rare, by their nature, which means we have less data to validate that range of our scale. Also, practically speaking there are floors and ceilings. Someone who gets a 20 on the TOEFL ibt and someone who gets a 30 share one most important thing: they're functionally unable to communicate in English. This is also why you shouldn't trust anyone who tells you they have an IQ over, say, 150 or so. The scale just doesn't mean anything up that high.)
How do we get these pretty normal distributions? That's the work of test development, and part of why it can be a seriously difficult and expensive undertaking. The nature of numbers (and the central limit theorem) help, but ultimately the big testing companies have to spend a ton of time and money getting a distribution as close to normal as possible - and whatever else their flaws, organizations like ETS do that very well. Either way, it's essential to say that the normal distribution does not arrange itself like magic in tests. It has to be produced with careful work.
The Question of Grades
Thinking about these two paradigms can help us think through some questions. Here's a simple one: are grades norm referenced or criterion referenced? The answer is surely both and neither, but I think it's useful to consider the dynamics here for a minute. In one sense, grades are clearly criterion referenced, in that they are meant to reflect a given student's mastery of the given course's subject matter. And we aren't likely to say that only X% of students in a class should pass or fail according to a model distribution; rather, we think we should pass everyone who demonstrates the knowledge, skills, and competencies a class is designed to instill. And we have little reason to think that grades are actually normally distributed between students in the average class.
Yet, in another sense, we clearly think of grades as norm referenced. When we talk about grade inflation, we are often speaking in terms of norm referencing, complaining that we're losing the ability to discriminate between different levels of ability. Grades are used to compare different students from remarkably different educational contexts in the college admissions process. And sometimes, we "curve a test," meaning adjusting a test to better match the normal distribution - which does not, contrary to undergraduate presumption, necessarily help the people who took the test. There's an intuitive sense that grades should match a fairness distribution that, while not normal around the natural mean (you wouldn't want the average grade to be a 50, I trust), still essentially replicates normality in that both very high and very low grades should be rare. In practice, this is not often the case. A's, in my experience, outnumber F's.
In grad school a perpetual concern was the very high average grade of freshman composition, something like a B+. And the downwards pressure on that average was largely the product of students who stopped coming to class and thus got F's, meaning that the average grade of students who actually completed the course was probably very high indeed. Is this a problem? I guess it depends on your point of view. If we were trying to meaningfully discriminate between different students based on their freshman comp grades, then certainly - but I'm not sure if we'd want to do that. On the other hand, it might be that freshman comp is a class that we think most students might naturally be expected to do well; it isn't written anywhere that the criterion for success be at a particularly high level. Certainly the major departments wouldn't like too many students failing that Gen Ed, given that they'd then have to fill valuable schedule space when they retook it. The question, though, is whether those grades actually reflect a meaningful meeting of the given benchmarks - fulfilling the criterion. I'm of the opinion that the answer is often "no" when it comes to freshman comp, meaning that the average grades are probably too high no matter what.
I don't have any grand insight here, and I think most people are able to meaningfully think about grades in a way that reflects both norm-referenced and criterion-referenced interests. But I do think that these dynamics are important to think about. As I've been saying lately, I think that there are some basic aspects of education and education policy that we simply haven't thought through adequately, and we all could benefit from going back to the basics and pulling apart what we think we want.