Beware Berkson's Paradox

scatterplot by Adam Strandberg via Brilliant

There’s a lot of populist data science going on right now thanks to Covid-19. That might make you wince, given all the cranks and conspiracy theorists out there. But ordinary people interpreting data is inevitable; democracy pretty much requires us to be amateur scientists right now, and with so much controversy out there, it’s important to informed. The cranks and conspiracy theorists aren’t going to just stop, after all. Better to cultivate a respect for the work we all need to do in order to better understand where we are with this disease. (Distrust anyone who thinks less citizen thinking is better than more.) But it’s hard! It’s easy to go wrong, even excluding those who are actively dishonest, and we are living in the culture war consequences of that difficulty. We’re all trying to navigate this the best we can. Which does not, obviously, mean that everyone is doing it equally well.

As with all things in this domain, I come from a position of being something a little more than an amateur but far from an expert. I have a lot of formal academic training in research methods and some in statistics, along with a little serious research experience, but I’m mostly just a math-illiterate person who finds this stuff cool and likes to learn about it. In the spirit of all of us getting a little more informed, I’ll share something I've read about in several places and thought was interesting, with the caveat that if you find it interesting too you should read people who know more.

What I worry about a lot, when tendentious Covid stats are floating around, is Berkson’s paradox. I don’t have a specific example of this potential pitfall has popped up in Covid discussion yet, but I’m on the lookout for this dynamic. I keep seeing on social media “facts” of the type “hospitalized vaccinated patients under 50 are twice as likely to die than unvaccinated!” This cries out for information on the basal rates for infection, hospitalization, and death for each subgroup there, among other things. But it also should make us nervous about how the various studied samples are getting put together in the data. Berkson’s paradox, defined broadly, refers to the tendency of subpopulations caused by some selection effect such as a cut-score to produce the impression of correlations that don’t exist, or even exist in the opposite direction, in the broader population.

We’ll put this in simple, (almost) math-free terms. Let’s say we’re looking for a Product to buy, and that there are two attributes about the Product we care about. We weigh the two attributes equally, and we’ll call them X and Y. X and Y are both on a binary low-high scale. We’re pretty lenient - we only need the Product to be rated high on either X or Y for us to buy it. So we go out and buy all the products with a single high, not paying attention to the numbers now, just grabbing our sample. Unbeknownst to us, across all of the Products there’s an equal portion with both high or low and with one high and one low. So….

• High X - high Y combinations (25%) are bought

• High X - low Y combinations (25%) are bought

• Low X - high Y combinations (25%) are bought

• Low X - low Y combinations (25%) are rejected

We feel we've got a good sample of Products to research. Now we want to explore the association between X and Y, that is, whether Products that are high/low in one tend to be high/low in the other. At first glance you might assume that there’s no relationship - among all Products, there’s equal amounts where both are high/low and where one is low and one high, that is, as many examples where they vary together as where they diverge. But remember, low X - low Y got rejected and that 25% of the initial data is not in our sample. So 66.6% of our remaining sample is low/high or high/low, and 33.3% of our remaining sample is high/high. This would markedly change the perceived relationship between X and Y; now, in our sample, there’s twice as many Products where they diverge than where they vary together, and we might assume that therefore there’s a strong trend for them to diverge in the population rather than to vary together. But that relationship doesn’t exist across all Products. The cut score is preventing us from seeing the bigger picture of the association we care about. It’s a statistical mirage. That’s Berkson’s paradox.

Or, as Wikipedia succinctly puts it, “given two independent events, if you consider only outcomes where at least one occurs, then they become negatively dependent.” The most general definitions of Berkson’s paradox (sometimes Berkson’s bias) I’ve seen equate it with selection effects in general, but I think it’s mostly used in situations where you’re excluding a part of the population/dataset that would reduce or reverse the observed correlation if included. It’s also related to conditioning on a collider.

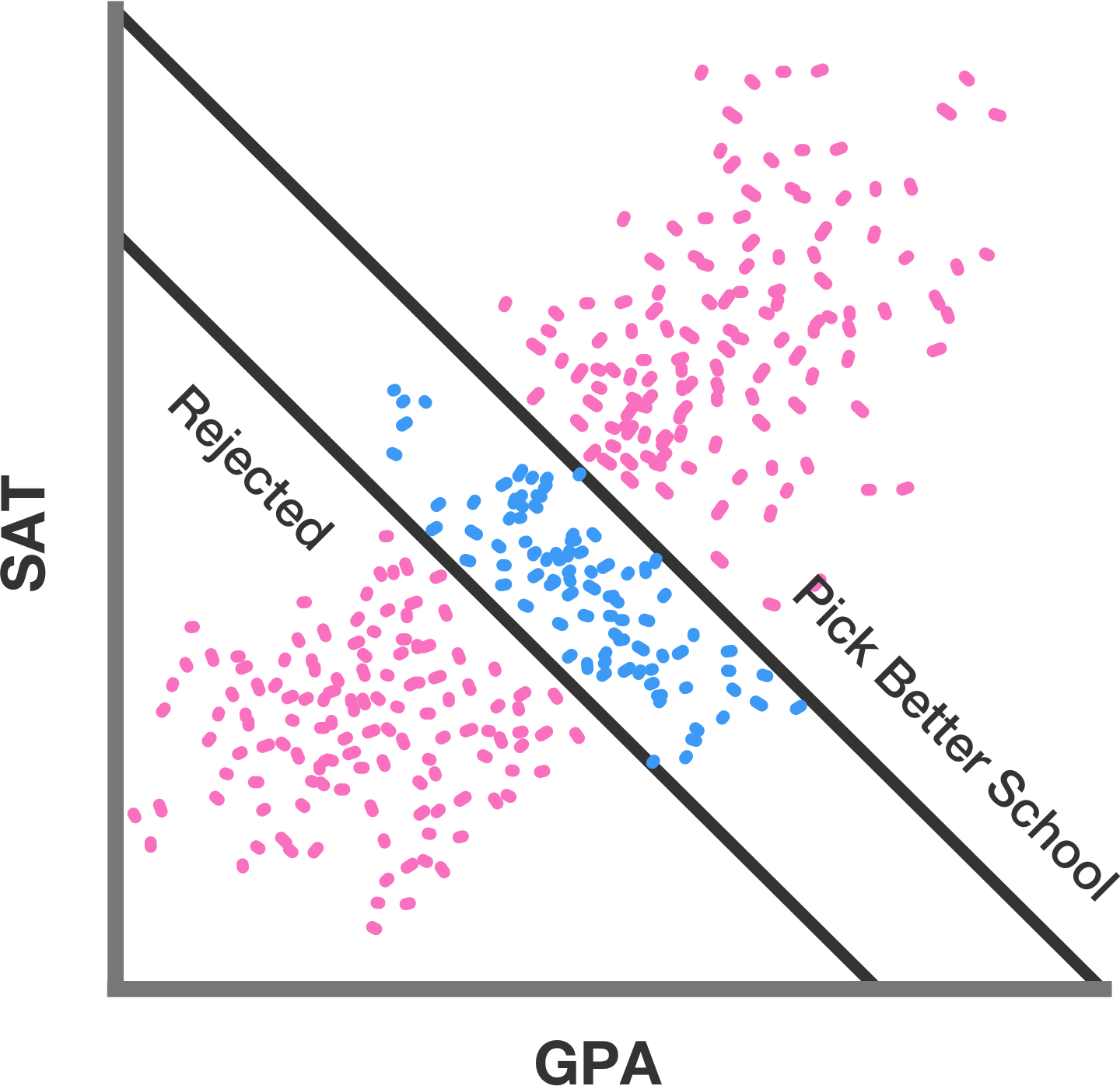
This invented scenario allows us to see the general effect without adding the complication of real data. You can imagine, though, how even far noisier (ie more realistic) data could present the same challenges - if whatever cut-score we’re using eliminates a significant portion of the population where the variables in question have a strong tendency to vary together/diverge, that removal will change the observed relationship in the opposite direction. As I’ve said several times here before, the raw correlation between SAT scores and freshman year GPA is artificially depressed, as only people who go to college are in that analysis, but the subpopulation of those who don’t go is filled with many people who scored low on the SATs and would have struggled in college. In my invented buying Products scenario the problem is obvious and we could have more carefully gathered data about X and Y before buying. But in many scenarios we can’t have data before selection; if you’re a college administrator you only have data from your own students, and not from those who don’t enroll, and anyway “college GPA” is not a variable that exists for people who don’t go to college. This is one of the tricky elements of dealing with this kind of problem, asking yourself “Am I really interested only in the relationship within my sample, or am I in any sense extrapolating to the broader population?”

I’ve read that an example of Berkson’s Paradox lies in the relationship between height and basketball ability. Supposedly in the NBA there’s no relationship between various summative quantitative measures of a player’s value such as PER or win shares and their height. I have no idea if this is true, but it fits my loose impression. Giannis Antetokounmpo (7’) is really good but so is James Harden (6’5) and so is Chris Paul (6’0), after all. But this is kind of crazy, right? Of course being tall is no guarantee of being good at basketball and being short no guarantee of being bad, but also most people who are elite basketball players are really crazy tall. In fact, being tall is so important to basketball, and extreme height so rare, that better than 15% of American 7 footers play in the NBA. Yet this correlation apparently does not exist when we restrict our analysis to the NBA.

The obvious Berkson’s Paradox reading is that people who are good at basketball and short and people who are bad at basketball and tall can make the NBA, but people who are short and bad at basketball have been cut out of the sample by the intense competition. It’s hard for me to put it in those terms; even the most clumsy Shawn Bradley-style centers are magnificent athletes, and of course players like Wilt Chamberlain were transcendent. But it’s true that there’s just a vastly larger population of 6 footers than 7 footers, meaning more opportunities to hit the slim odds of having NBA-level talent. With far fewer 7 footers there's far fewer rolls of the talent dice and more likelihood of rostering a less-skilled player. That could create the conditions necessary for very tall but low-skilled players to make the league without being balanced out by short and low-skilled players who don’t.

In the broader sense, though, we could call this a Berkson effect just through the general application of unusual selection forces likely creating unexamined relationships. The NBA is a crazy tiny slice of the overall basketball playing population. Every person who makes it to the league is an insanely skilled genetic marvel that’s been through a decades-long process of evaluation by coaches and scouts. Overall trends just don’t always apply to populations with such intense selection effects. Being tall is a major component of being successful at basketball, but at the NBA level you also have to have elite explosiveness, elite skill, elite vision…. The salience of these rare attributes in the NBA can easily overpower the value of height observed in the broader population.

The question is, what are the potential Berkson’s paradox problems with Covid? I’m not sure, though I bet commenters will list some possibilities for us. But these data interpretation issues are well-known in epidemiology, and I know they’re lurking somewhere. To go back to that social media claim, maybe hospitalized (a subpopulation, and one with a basal rate different from the population) vaccinated (same) under-50 (same) patients really do die at twice the rates of the unvaccinated. But what does that really tell us, given what we know about the vagaries of sampling in such a scenario? I would be very careful when drawing inferences from data with so many selection effects/cutpoints. In general I suggest we all think about basal rates, cutpoints, and excluded portions of sampled populations as we continue to stumble our way through this pandemic.

(If that's not a sexy closing sentence, I don't know what is.)