One persistent way that human beings misrepresent the world is through the gambler's fallacy, and there's a kind of implied gambler's fallacy that works its way into journalism quite often. It's hugely important to anyone who cares about research and journalism about research.
The gambler's fallacy is when you expect a certain periodicity in outcomes when you have no reason to expect it. That is, you look at events that happened in the recent past, and say "that is an unusually high/low number of times for that event to happen, so therefore what will follow is an unusually low/high number of times for it to happen." The classic case is roulette: you're walking along the casino floor, and you see the electronic sign showing that a roulette table has hit black 10 times in a row. You know the odds of this are very small, so you rush over to place a bet on red. But of course that's not justified: the table doesn't "know" it has come up black 10 times in a row. You've still got the same (bad) odds of hitting red, 47.4%. You're still playing with the same house edge. A coin that's just come up heads 50 times in a row has the same odds of being heads again as being tails again. The expectation that non-periodic random events are governed by some sort of god of reciprocal probabilities is the source of tons of bad human reasoning - and journalism is absolutely stuffed with it. You see it any time people point out that a particular event hasn't happened in a long time, so therefore we've got an increased chance of it happening in the future.
Perhaps the classic case of this was Kathryn Schulz's Pulitzer Prize-winning, much-celebrated New Yorker article on the potential mega-earthquake in the Pacific northwest. This piece was a sensation when it appeared, thanks to its prominent placement in a popular publication, the deftness of Schulz's prose, and the artful construction of her story - but also because of the gambler's fallacy. At the time I heard about the article constantly, from a lot of smart, educated people, and it was all based on the idea that we were "overdue" for a huge earthquake in that region. People I know were considering selling their homes. Rational adults started stockpiling canned goods. The really big one was overdue.
Was Schulz responsible for this idea? After publication, she would go on to be dismissive of the idea that she had created the impression that we were overdue for such an earthquake. She wrote in a followup to the original article,
Are we overdue for the Cascadia earthquake?
No, although I heard that word a lot after the piece was published. As DOGAMI’s Ian Madin told me, “You’re not overdue for an earthquake until you’re three standard deviations beyond the mean”—which, in the case of the full-margin Cascadia earthquake, means eight hundred years from now. (In the case of the “smaller” Cascadia earthquake, the magnitude 8.0 to 8.6 that would affect only the southern part of the zone, we’re currently one standard deviation beyond the mean.) That doesn’t mean that the quake won’t happen tomorrow; it just means we are not “overdue” in any meaningful sense.
How did people get the idea that we were overdue? The original:
we now know that the Pacific Northwest has experienced forty-one subduction-zone earthquakes in the past ten thousand years. If you divide ten thousand by forty-one, you get two hundred and forty-three, which is Cascadia’s recurrence interval: the average amount of time that elapses between earthquakes. That timespan is dangerous both because it is too long—long enough for us to unwittingly build an entire civilization on top of our continent’s worst fault line—and because it is not long enough. Counting from the earthquake of 1700, we are now three hundred and fifteen years into a two-hundred-and-forty-three-year cycle.
By saying that there is a "two-hundred-and-forty-three-year cycle," Schulz implied a regular periodicity. The definition of a cycle, after all, is "a series of events that are regularly repeated in the same order." That simply isn't how a recurrence interval functions, as Schulz would go on to clarify in her followup - which of course got vastly less attention. I appreciate that, in her followup, Schulz was more rigorous and specific, referring to an expert's explanation, but it takes serious chutzpah to have written the preceding paragraph and then to later act as though there's no reason your readers thought the next quake was "overdue." The closest thing to a clarifying statement in the original article is as follows:
It is possible to quibble with that number. Recurrence intervals are averages, and averages are tricky: ten is the average of nine and eleven, but also of eighteen and two. It is not possible, however, to dispute the scale of the problem.
If we bother to explain that first sentence thoroughly, we can see it's a remarkable to-be-sure statement - she is obliquely admitting that since there is no regular periodicity to a recurrence interval, there is no sense in which that "two-hundred-and-forty-three-year cycle" is actually a cycle. It's just an average. Yes, the "really big one" could hit the Pacific northwest tomorrow - and if it did, it still wouldn't imply that we've been overdue, as her later comments acknowledge. The earthquake might also happen 500 years from now. That's not a quibble; it's the root of the very panic she set off by publishing the piece. But by immediately leaping from such an under-explained discussion of what a recurrence interval is and isn't to the irrelevant and vague assertion about "the scale of the problem," Schulz ensured that her readers would misunderstand in the most sensationalistic way possible. However well crafted her story was, it left people getting a very basic fact wrong, and was thus bad science writing. I don't think Schulz was being dishonest, but this was a major problem with a piece that received almost universal praise.
I just read another good example of an implied gambler's fallacy in a comprehensively irresponsible Gizmodo piece on supposed future pandemics. I am tempted to just fisk the whole thing, but I'll spare you. For our immediate interests let's just look at how a gambler's fallacy can work by implication. George Dvorsky:
Experts say it’s not a matter of if, but when a global scale pandemic will wipe out millions of people.... Throughout history, pathogens have wiped out scores of humans. During the 20th century, there were three global-scale influenza outbreaks, the worst of which killed somewhere between 50 and 100 million people, or about 3 to 5 percent of the global population. The HIV virus, which went pandemic in the 1980s, has infected about 70 million people, killing 35 million.
Those specific experts are not named or quoted, so we'll have to take Dvorsky's word for it. But note the implication here: because we've had pandemics in the past that killed significant percentages of the population, we are likely to have more in the future. An-epidemic-is-upon-us stories are a dime a dozen in contemporary news media, given their obvious ability to drive clicks. Common to these pieces are the implication that we are overdue for another epidemic because epidemics used to happen regularly in the past. But of course, conditions change, and there's few fields where conditions have changed more in the recent past than infectious diseases. Dvorsky implies that they have changed for the worse:
Diseases, particularly those of tropical origin, are spreading faster than ever before, owing to more long-distance travel, urbanization, lack of sanitation, and ineffective mosquito control—not to mention global warming and the spread of tropical diseases outside of traditional equatorial confines.
Sure, those are concerns. But since he's specifically set us up to expect more pandemics by referencing those in the early 20th century, maybe we should take a somewhat broader perspective and look at how infectious diseases have changed in the past 100 years. Let's check with the CDC.
The most salient change, when it comes to infectious, has been the astonishing progress of modern medicine. We have a methodology for fighting infectious disease that has saved hundreds of millions of lives. Unsurprisingly, the diseases that keep getting nominated as the source of the next great pandemic keep failing to spread at expected rates. Dvorsky names diseases likes SARs (global cases since 2004: zero) and Ebola (for which we just discovered a very promising vaccine), not seeming to realize that these are examples of victories for the control of infectious disease, as tragic as the loss of life has been. The actual greatest threats to human health remain what they have been for some time, the deeply unsexy threats of smoking, heart disease, and obesity.
Does the dramatically lower rate of deaths from infectious disease mean a pandemic is impossible? Of course not. But "this happened often in the past, and it hasn't happened recently, so...." is fallacious reasoning. And you see it in all sorts of domains of journalism. "This winter hasn't seen a lot of snow so far, so you know February will be rough." "There hasn't been a murder in Chicago in weeks, and police are on their toes for the inevitable violence to come." "The candidate has been riding a crest of good polling numbers, but analysts expect he's due for a swoon." None of these are sound reasoning, even though they seem superficially correct based on our intuitions about the world. It's something journalists in particular should watch out for.

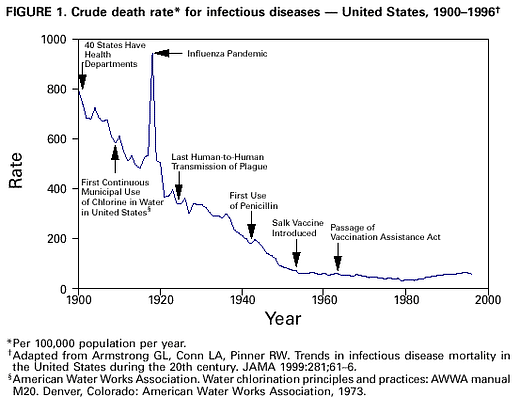


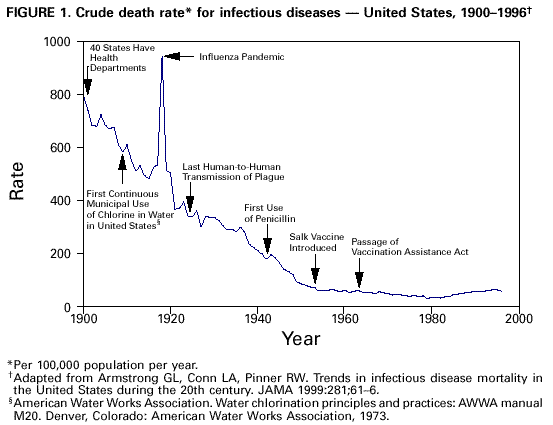
Although I have a BSc in Math and have taken stats courses in grad school, I am no expert in probability. And I have only a layman’s knowledge earthquakes, so I am hoping others with more knowledge will correct any of the following.
First, to Ian Madin's view that we would not be "overdue" for an earthquake until we were three standard deviations from the mean. In a normal distribution (which the occurrence of earthquakes is not) three standard deviations above the norm means that 99.7% of the data points are below that. If a woman is at the third standard deviation for female height, she is taller than 99.7% of all women.
For earthquakes, the metric is number of years since the last one. To be at the third standard deviation, means that in all other cases, 99.7% of the quakes would have happened by now. I would suggest that this would mean a quake is more than “overdue”. It is very, very likely in the next few years.
The other point: the Gambler’s Fallacy depends on the spins of the roulette wheel being independent. Historical results have no bearing on the next spin. I explain this to people by suggesting that if I took a quarter out of my pocket and flipped it, what would be the probability of a head? If history mattered, we would have no idea because we do not know where that quarter has been and how many times it may have been flipped (OK, this is pretty well what you said. I just want to emphasize the importance of the events being independent). In fact, if a roulette wheel had produced 10 blacks in a row, your best bet would be black as there would be some evidence that the wheel may not be fair.
Years since the last earthquake are NOT independent. As time goes on, the pressure in the tectonic plates builds up and a quake becomes more likely. In the first few years after a big one, the pressure is off and the chance of another big one is essentially zero. So, to say that because there has not been a Big One from the Cascadia Fault since 1700, we are closer to the major destructive earthquake is not wrong.
I suspect, too, that as time goes on, the next quake is more likely to be a big one as the pressure has built up creating more potential energy for when the fault finally gives.